Dynamic programming (DP) is a technique to solve polynomial problems through the reuse idea. It's similar to divide-and-conquer where you will break to the smaller problem and reuse the results to find the final solution.

diagrama.png
Font: GeeksForGeeks


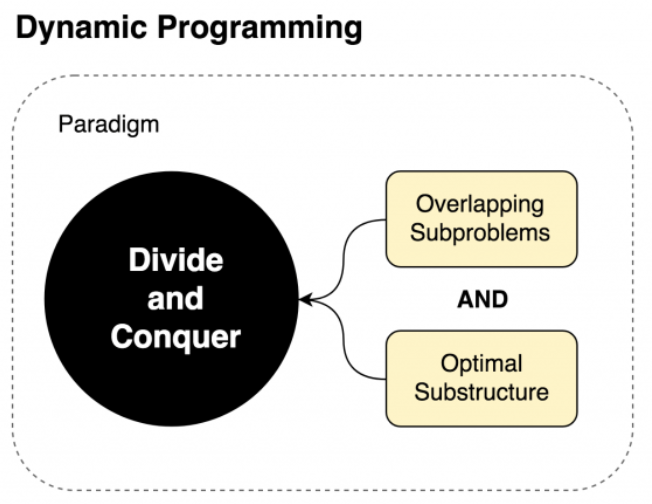
Usually, problems to maximize or minimize can be solved using DP. However, to a problem to be considered a DP it needs to fit with certain restrictions or prerequisites. Then, to a problem to be considered solved by DP it has to have:

  • optimal substructure: optimal solution can be constructed from optimal solutions of its subproblems
  • overlapping sub-problem: the problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblems. The techniques to resolve the problems are memorization and tabulation.

If a problem doesn't fit with these two attributes it's just in the divide-and-conquer strategy. That's why the merge sort and quick sort are not classified as dynamic programming problems.

We can summarize how to identify if a problem solved using DP in the steps:

  1. Identify problem variables
  2. Clearly express the recurrence relation
  3. Identify the base cases
  4. Decide if you want to implement it iteratively or recursively

Steps 1, 2 and 3 are related to the state of the transition. Then, the DP is regarding find a relation between previous states and the current state.

  • State: A state can be defined as the set of parameters that can uniquely identify a certain position or standing in the given problem. This set of parameters should be as small as possible to reduce state space.

One example is the Fibonacci problem [1][2]. Using recursive solution the time complexity is O(2^n) while the DP solution only O(n).

//  1 1 2 3 5 8 13 21 34 56 90
public class Fibonacci {

  private static int number;
  private Integer cache[];

  public static void main(String[] args) {

    number = 9;

    Fibonacci fact = new Fibonacci();
    System.out.println(fact.fibonacciRecursive(number));
    System.out.println(fact.fibonacciIterative(number));
  }

  public int fibonacciRecursive(int number) {
    if (number <= 1) {
	    return number;
    }
    return fibonacciRecursive(number - 1) + fibonacciRecursive(number - 2);
  }

  public long fibonacciIterative(int number) {

    int f[] = new int [number + 2];
    f[0] = 0;
    f[1] = 1;

    for (int i = 2; i <= number; i++) {
      f[i] = f[i -1] + f[i-2];
    }

    return f[number];
  }

  public int cacheFibo(int number) {

    Integer cache[] = getCache();

    if (cache[number] == null) {
      cache [number] = cacheFibo(number-1) + cacheFibo(number-2);
    }

    return cache[number];
  }

  private Integer[] getCache() {
    if(cache == null) {
      cache = new Integer [number];
    }
    return cache;
  }

}

The first method (fibonacciRecursive) solves the problem using the memorization idea, with recursive calls and star the state in N (TopDown). The second method (fibonacciIterative) uses the tabulation idea with the initial state started by '1' (BottomUp). The first strategy is easier to think and implement, however, it uses recursivity, which makes the second one, the iterative way, faster than the first method.

The solution can be improved using cache. The last method (cacheFibo) show that.

Recursion: Pay Attention to the stack

You have to pay attention how you are using the recursion. When the values are bing passed to be calculate on the end of the process you will have a stack with many values. It can throw errors because of a full stack.

The example bellow (fibonacci) show how the stack is going to be used to process all the result in the end, going back each step when have values the be processed.

//5! = 5*4*3*2*1
public class Factorial {

  public static void main(String[] args) {
    Factorial fact = new Factorial();
    System.out.println(fact.factorialRecursive(5));
    System.out.println(fact.factorialRecursive(5,1));
    System.out.println(fact.factorialIterative(5));
  }

  public long factorialRecursive(int number) {
    if (number == 2) {
      return 2;
    }
    System.out.println(number + " * factorialRecursive(" + (number - 1) + ")" );
    long result  =  number * factorialRecursive(number - 1);
    System.out.println("Partial Result: " +  number + " * factorialRecursive(" + (number - 1) + ")" );
    return result;
  }

  public long factorialRecursive(int number, int a) {
    if (number <= 1) {
      return a;
    }
    return factorialRecursive( number - 1, number * a);
	}

  public long factorialIterative(int number) {

    if (number == 0 || number == 1) {
      return 1;
    }

    int result = 1;

    for (int i = 2; i <= number; i++) {
      result *= i;
    }

    return result;
  }
}

The outcome from the first recursive code is printed bellow where you will see the stack being completed with data to calculate everything in the end, removing data from the stack.

// Storage data on stack
5 * factorialRecursive(4)
4 * factorialRecursive(3)
3 * factorialRecursive(2)

// Go down in the stack calculating values
3 * factorialRecursive(2)
4 * factorialRecursive(3)
5 * factorialRecursive(4)

// Result
120

The second recursive code is a memory improvement where the values is already calculate. It makes not necessary storage the data.

Here is a good explanation how happen this use of stack by recursion.

Conclusion

Dynamic Programming is a great resource to improve performance in complex problems and recursion is good support. However, the recursion can give memory problem is not have a good implementation.

Also, you can see other algorithms that use the DP: QuickSort and MergeSort.

Reference